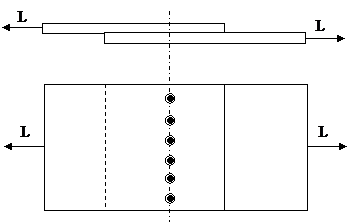
Example:
Determine the safe tensile, shear and bearing loads and the efficiency for a 300 mm section of single-riveted lap joint made from ¼” plates using six 16-mm diameter rivets. Assume that the drilled holes are 1.5 mm larger in diameter than the rivets. The values for the design limits for tensile, shear and bearing stress can be taken as 75, 60 and 131 MPa, respectively.
|
|
Solution:
The safe tensile load, L, based on shear of the rivets is given by
L = n Ar τd = 6 π (0.0162 / 4) x 60 x 106 = 72.38 kN
The safe tensile load based on bearing pressure or compressive stress is given by
L = (Abearing) σ bearing = ( n x t x d) σ bearing
t = ¼ x 25.4 = 6.35 mm
L = (6 x 0.016 x (6.35 x10-3)) x 131 x 106 = 79.86 kN
The safe load based on tensile load is given by
L = Ap σt
The area of the plate between the rivet holes, Ap is given by
Ap = 0.00635 x (0.3 – 6 x (16 x 10-3 + 1.5 x 10-3)) = 1.238 x 10-3 m2
L = Ap σt = 1.238 x 10-3 x 75 x 106 = 92.87 kN
The safe tensile load would be the least of the three values determined, i.e.
L = 72.38 kN
η = 72.38 x 103 / (0.00635 x 0.3 x75 x 106) = 0.5066
The efficiency is 50.66%