Homework 4

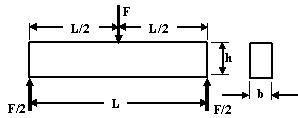
Example 1:

A rectangular beam 60 mm wide and 150 mm deep is simply supported over a span of 6 m. If the beam is subjected to central load of 12 kN, find the maximum bending stress induced in the beam section.

Given:

            b = 60 mm

            h = 150 mm

            L = 6 m = 6 000 mm

    W = F = 12 kN = 12 000 N

Req:

             σ_{b max} = ?

Solution:

              σ_{b max} = (M_max y_max)/(I_min) ………..(1)

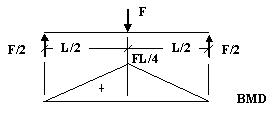
M_max = FL/4 = (12 000 x 6 000) / 4 = 18 000 000 Nm

Y_max = h/2 = 150/2 = 75 mm

I_min= I= bh³/12 = (60 x 150³) /12 = 16875000 mm⁴

From eqn. (1)
                        σ_{b max} = (18 000 000 x 75)/ 16 875 000

                         σ_{b max} = 80 MPa (Ans.)

σ_{b max} = 80 MPa

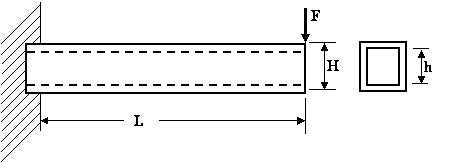
1- A cantilever beam is rectangular in section having 80 mm width and 120 mm depth. If the cantilever is subjected to a point load of 6 kN at the free end and the bending stress is not to exceed 40 MPa, find the span of the cantilever beam (1.28 m)

2- A Hollow square section with outer and inner dimensions of 50 mm and 40 mm respectively is used as a cantilever of span 1 m. How much concentrated load can be applied at the free end of the cantilever, if the maximum bending stress is not to exceed 35 MPa? (430.5 N)

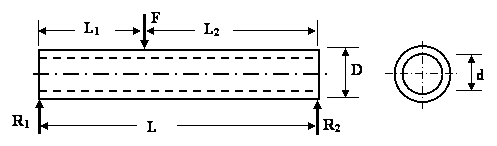
3- A hollow steel tube having external and internal diameter of 100 mm and 75 mm respectively is simply supported over a span of 5 m. The tube carries a concentrated load of F at distance of 2 m from one of the supports. What is the value of F, if the maximum bending stress is not to exceed 100 MPa. (5.6 kN)