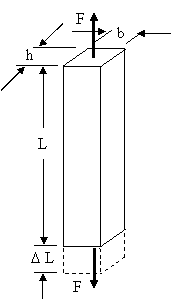Homework 1
Ex 1) A steel rod 1 m long and 20 mm x 20 mm in cross-sectional is subjected to a tensile force of 40 kN. Determine the elongation of the road, if modulus of elasticity for the rod material is 200 GPa.
|
Give: b = 20 mm h = 20 mm L = 1 m = 1 000 mm F = 20 kN = 40 000 N E = 200 GPa = 200 000 MPa
Req.: DL = ?
Solution: |
|
|
σ = F / A
A = b x h = 20 x 20 = 400 mm2
σ = F/A = 40 000/400 = 100 MPa
E = σ / e
e = DL / L E = σ /(DL / L) = σ L / DL 200 000 = 100 x 1 000 / DL DL = 100 x 1 000 / 200 000 = 0.5 mm (Ans.) |
DL = 0.5 mm |
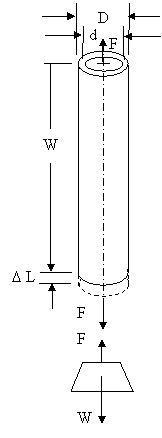
Ex 2) A hollow cylinder 2 m long has an outside diameter of 50 mm and inside diameter of 30 mm. If the cylinder is carrying a load of 25 kN, find the stress in the cylinder. Also find the deformation of the cylinder, if the value of modulus of elasticity for the cylinder material is 100 GPa.
|
Given:
L = 2 m = 2 000 mm D = 50 mm d = 30 mm W = 25 kN = 25 000 N = F E = 100 GPa = 100 000 MPa
Req:
σ = ?
D L = ?
Solution:
|
|
|
A = (p/4) D2 – (p/4) d2 = (p/4) (D2 –d2)
= (p/4) (502 –302) = 1257 mm2
σ = F/A = 25 000 / 1257 = 19.9 MPa (Ans.) E = σ / e = σ / (D L / L) = σ L / 20 000 = 19.9 x 2 000 / D L D L = 19.9 x 2 000 / 100 000 = 0.398 mm = 0.4 mm (Ans.) |
σ = 19.9 MPa
D L = 0.4 mm |
1) A load of 5 kN is to be raised with the help of a steel wire. Find the minimum diameter of the steel wire, if the stress is not to exceed 100 MPa. Also find the strain in the wire if its length is 2 m, if modulus of elasticity of the wire diameter is 220 GPa. (d = 7.98 mm » 8 mm, e = 4.55x10-4)
2) In an experiment, a steel specimen of 13 mm diameter was found to elongate 0.2 mm in a 200 mm gauge length when it was subjected to a tensile force of 26.8 kN. If the specimen was tested within the elastic range, what is the value of Young’s modulus for the steel specimen? (E = 201.9 GPa)
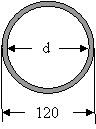
3) A hollow steel tube 3.5 m long has external diameter of 120 mm. In order to determine the internal diameter, the tube was subjected to a tensile load of 400 kN and extension was measured to be 2 mm. If the modulus of elasticity for the tube material is 200 GPa, determine the internal diameter of the tube. (d = 99.71 mm)
4) Two wires, one of steel and the other of copper, are of the same length and are subjected to the same tension. If the diameter of the copper wire is 2 mm, find the diameter of the steel wire, if they are elongated by the same amount. Take E for steel as 200 GPa and that for copper as 100 GPa. (ds = 1.41 mm)
5) A steel bar 2 m long and 150 mm2 in cross-section is subjected to an axial pull of 15kN. Find the elongation of the bar. Take E = 200 GPa. (dL = 1.0 mm)
6) A straight bar of 500 mm length has its cross-sectional area of 500 mm2. Find the magnitude of the compressive load under which it will decrease its length by 0.2 mm. Take E for the bar material as 200 GPa. (F = 40 kN)
7) An alloy bar 1 m long and 200 mm2 in cress-section is subjected to a compressive force of 20 kN. If the modulus of elasticity for the alloy is 100 GPa, find the decrease in length of the bar. (dL = - 1.0 mm)
8) A hollow cylinder 4 m long has outside and inside diameters of 75 mm and 60 mm respectively. Find the stress and deformation of the cylinder, when it is carrying an axial tensile load of 50 kN. Take E =100 GPa. (σ = 31.4 MPa, dL = 1.26 mm)
Homework 2
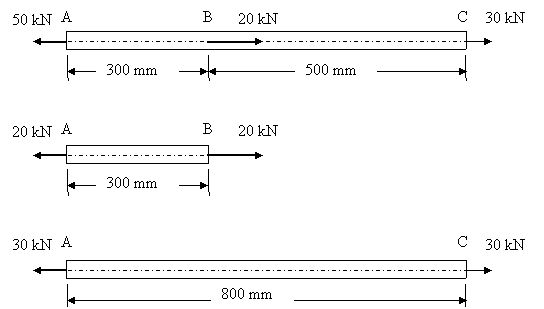
Ex 1) A steel bar of cress-sectional area of 200 mm2 is loaded as shown in the figure. Find the change in length of the bar. Take E as 200 GPa.

Given:
A= 200 mm2
E = 200 GPa = 200 000 MPa
Req.:
DL = ?
Solution:
:
|
E = σ / e = (F/A) / (DL/L) = (F L) / (A DL)
DL1 = (F1 L1) / ( A E)
DL2 = (F2 L2) / ( A E)
DL = () / ( A E) + (F2 L2) / ( A E)
DL = 1 / (A E) (F1 L1 + F2 L2)
DL = [1/ (200 x 200 000)] (20 000 x 300 + 30 000 x 800)
DL = 0.75 mm (Ans.) |
DL = 0.75 mm |
1) A brass bar, having cross-sectional area of 500 mm2 is subjected to axial forces as shown in the figure. Find the total elongation of the bar. Take E = 80 GPa. (dL = 0.85 mm)

2) A steel rod ABCD 4.5 m long and 25 mm in diameter is subjected to the forces as shown in the figure. If the value of Young’s modulus for the steel is 200 GPa. Determine its deformation. (dL = 2.70 mm)