Example:

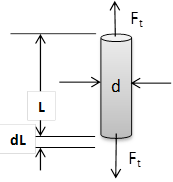
A tensile load of F_t = 24 kN is applied on a L = 160 mm

cylindrical rod made of steel EN8,and has a diameter d=20 mm.

Taking a factor of safety SF = 6, Find if the tensile stress on the

rod exceeds the allowable stress or not.

Also, find the increase of rod length (dL) due the tensile load,

where the steel’s modulus of elasticity E = 190 GPa.

Find the optimum design for the rod. A) Material, B) Dimensions.

Given:

F_t = 24000 N

d = 20 mm

FS = 6

E = 190 GPa

Req.:

- If σ_t < σ_all or   σ_t > σ_all

- dL

Solution:

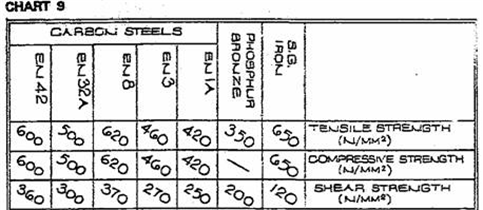
From Chart 9

σ_u = 620 MPa

σ_all = σ_u / SF = 620/6 = 103.33 MPa

σ_t = F/A = F/(π/4 d²) = 24000/(π/4 20²)
    = 24000/314.16 =76.39 MPa

σ_t < σ_all  (OK)                                                                                        OK

E = σ_t /ε =  σ_t /(dL/L)

dL/L = σ_t / E = 76.39/190000 = 4.02 x10^-4

dL = 4.02 x10^-4 L = 4.02 x10^-4 x 160 = 0.064 mm                              dL = 0.064 mm

A) Choose another material, d = 20 mm:

σ_all = σ_t = 76.39 MPa

σ_u = σ_all x SF = 76.39 x 6 = 458.34 MPa

From Chart 9 we choose steel EN3 (σ_u = 460)                                    EN3

B) Change rod dimensions, (EN8):

σ_t = σ_all = 103.33 MPa

σ_t = F_t /A

A = F_t / σ_t = 24000/103.33 = 232.27 mm²

π/4 d² = 232.27 mm²

d = SQRT(4 x 232.27 / π ) = SQRT(295.73) = 17.2 mm                     d = 17.2 mm