Long Columns with Central Loading (Buckling)

A column failure is always sudden, total, and unexpected, and hence dangerous. There is no advance warning. A beam will bend and give visual warning that it is overloaded; but not so for a column.

The relation between the critical load and the column material and geometry is developed with reference to the figure shown. We assume a bar of length l loaded by a force p acting along the centroidal axis with different end conditions.

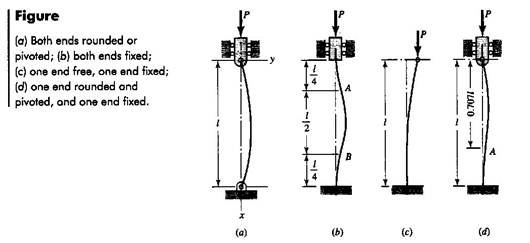
                                                                                       (1)

Equation (1) is called the Euler column formula,

where

P_cr = critical load (N)

C = end condition constant (see Table)

E = modulus of elasticity (N/m²)

I = second moment of area (m⁴)

l = shaft length (m)

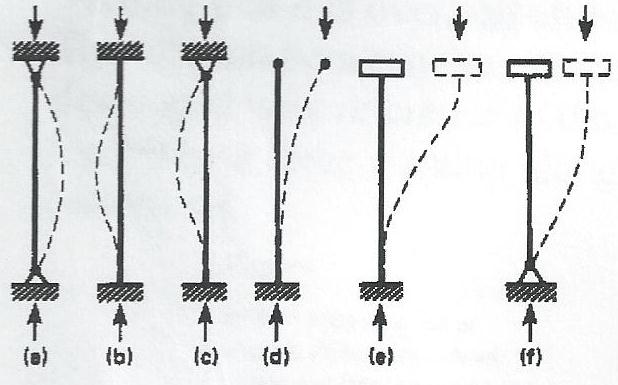
Table (Theoretical End Restraint Coefficients)

Illustration	End Conditions	C
(a)	Both ends pinned	1
(b)	Both ends built in	0.5
(c)	One end pinned, one end built in	0.707
(d)	One end built in, one end free	2
(e)	One end built in , one end fixed against rotation but free	1
(f)	One end pinned, one end fixed against rotation but free	2