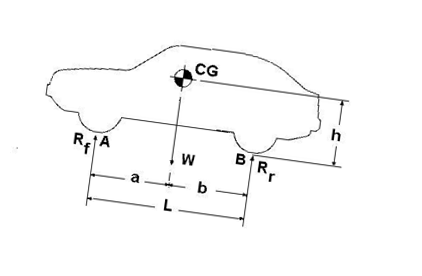
Finding the Car Center of Gravity (CG)

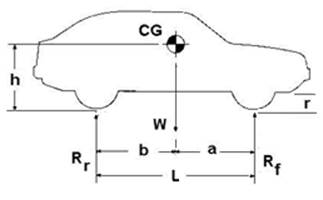
A. The longitudinal location of CG (a: the distance behind the front wheel, b: the distance in front of the rear wheel).

B. The height above ground of CG (h).

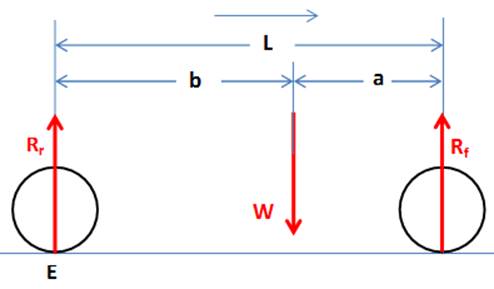
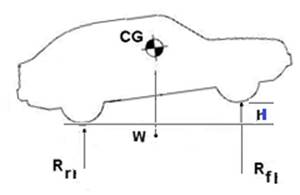
Fig. 1 The car on a level surface, L is the wheel base, (a and b are unknown longitudinal distances of the CG)	Fig. 2 The front wheels are raised up small distance H, r is the wheel radius, (h is the unknown distance of the CG height)

A:To determine the height of a vehicle's CG: Method 2

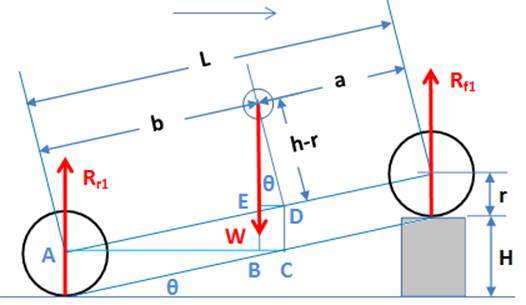
This method may be a little more difficult to understand, but if the rule of moments (force x perpendicular distance) is always applied, the calculations are quite easy. In practice no tilting platform is necessary, and only the axle loads are weighed while one pair of wheels are raised up quite a small distance h₁ (as shown in figure). The angle is measured by a clinometer or protractor, and then moments may be taken, making sure the above rule is applied. Taking moments about point A: 

Σ M_A = 0

R_{f 1} (L cos θ) - W (AB) = 0

then

R_{f 1} (L cos θ) = W (AB) ……….(1)

From the figure:

AB = AC – BC,

Where:

AC = b cos θ, and

BC = ED = (h-r) sin θ,

Then:

AB = AC – BC = b cos θ – (h-r) sin θ

From eq. (1)

R_{f 1} (L cos θ) = W (b cos θ – (h-r) sin θ)

b cos θ = AD cos θ = AC = AB +  BC = AB – ED

From figure;

AB = AC – BC

Since: 

AC =   b cos θ,  BC = ED = (h-r) sin θ

Then:

AB = b cos θ – (h-r) sin θ

Σ M_A = 0

R_f (L cos θ) - W (AB) = 0

R_f (L cos θ) = W (AB)

R_f - W [b cos θ – (h-r) sin θ] = 0

 W (h-r) sin θ = W b cos θ – R_f L cos θ

 h-r = [W (b cos θ) – R_f (L cos θ)] / [W sin θ]

h = {[W (b cos θ) – R_f (L cos θ)] / [W sin θ]} + r

where

θ = sin^-1 H/L

Worked  example

A vehicle having a mass of 2000 kg has a wheelbase of 2.42 m and its center of gravity lies1.52 m from the rear axle. The front end of the vehicle is lifted 35 cm and gives a mass reading of 1150 kg. The wheel radius is 30.5 cm. Determine the height of the CG.

θ = sin^-1 (35/242) = 8.31^o

h = [2000 (1.52) -1150 (242)] / [2000 tan (8.31)] + 0.305

h = m b – m_f L / m (H/(sqrt(L²- H²))

therefore         

F_l  x b cosq  = W_t . y₁ = W_t (y cosq - (h-r) sinq)

                   = W_t . y cosq - W_t .(h-r) sinq

then                

W_t (h-r) sinq  = W_t y cosq - F_l b cosq

therefore

(h-r) = (W_t y cosq - F_l b cosq)/(W_t sinq)

If masses are given they can be used instead of

weights, i.e. mass moments.

Worked  example

A vehicle having a mass of 2000 kg has a wheelbase of 2.42 m and its center of gravity lies1.52 m from the rear axle. The front end of the vehicle is lifted 35 cm and gives a mass reading of 1150 kg. The wheel radius is 30.5 cm. Determine the height of the CG.

In this case mass moments will be taken about the rear wheels

         sinq = h₁ /b = 0.35 /24.4 = 8.247^o

         cosq = 0.9896 and sin q = 0.1434

         h-r =  ( m cosq - F_l b cosq) / (m sinq)

               = ( 2000 x 1.52 x 0.9896 -1150 x 2.44 x 0.9896) / (2000 x 0.1434)

               = ( 3008 – 2777) / 286.8

               = 0.8054 m

thus     h = (h-r) + r

              = 0.8054 + 0.305

              =1.1104 m

Calculate the center of gravity location (a,b, and h) – Excel